-Hola de nuevo, ¿Listos para la última entrada sobre el tema de Conjuntos?-

Ya vimos en entradas anteriores formas de representar a los conjs, de qué están hechos (elementos y subconjuntos) y cómo podemos crearlos por medio de los Axs. Si aún no las has leído te invito a echarles un vistazo.

Ahora es el turno de ver cómo se comportan cuando se hacen operaciones de 2 o más conjs.

-Comencemos.-

Si \(X\), \(Y\) son conjuntos y \(z\) un elemento cualquiera:

Unión

\(X ∪ Y = z ∊ ⋃\){\(X, Y\)} \(= \){\(( z ∊ X) ∨ (z ∊ Y)\)}

En español esto quiere decir: z es un elemento que está en el conj X o z es un elemento que está en el conj Y.

Otra forma de decirlo: La unión es juntar a los elementos de los conjs que se están uniendo:

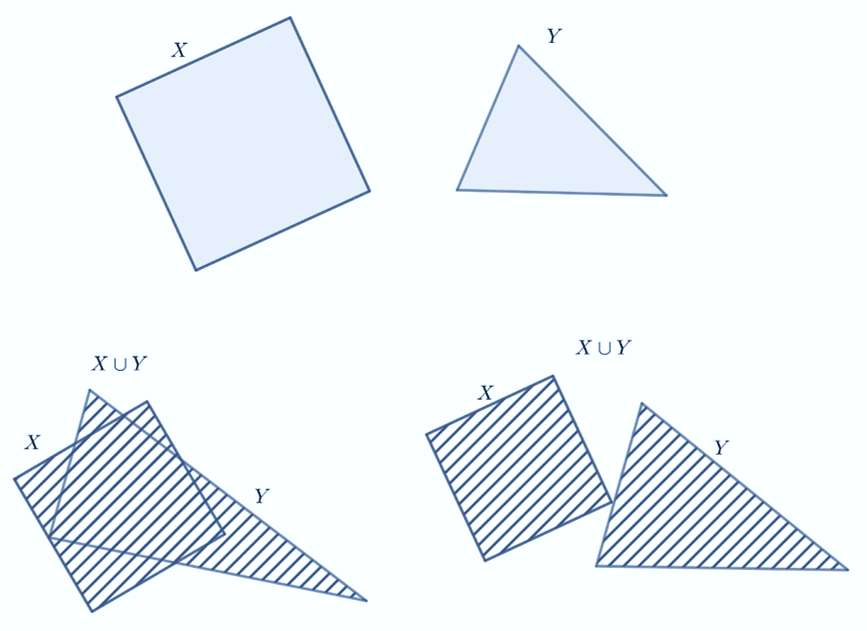
En dibujo, a la derecha se muestra la unión de conjs (disjuntos) que no tiene elementos en común, y a la izquierda conjs (que se intersecan) que sí tienen elementos en común. El elemento z se encuentra en el área rayada.

Al unir a los elementos de los dos conjs en el caso de que un elemento aparezca más de una vez después de hacer la operación, ese elemento únicamente se escribirá una sola vez. Esto es consecuencia de los Axs. del Par y de la Unión.

por ejemplo.

si \(X = \){\(1, 7\)} y \(Y = \){\(2,7\)}

Aquí el elemento que se repite es el número 7. Ya que aparece en ambos conjs:

\(X ∪ Y= \){\(1, 7\)} \(∪\) {\(2, 7\)} \(=\) {\(1, 2, 7, 7\)} \(=\) {\(1, 2, 7\)}

Intersección

\(X ∩ Y = z ∊ ⋂\){\(X, Y\)} \(=\) {\((z ∊ X) ∧ (z ∊ Y)\)}

En español esto quiere decir: \(z\) es un elemento del conj \(X\) y \(z\) es un elemento del conj \(Y\).

En otras palabras: La intersección de conjs busca a los elementos que tiene en común los conjs.

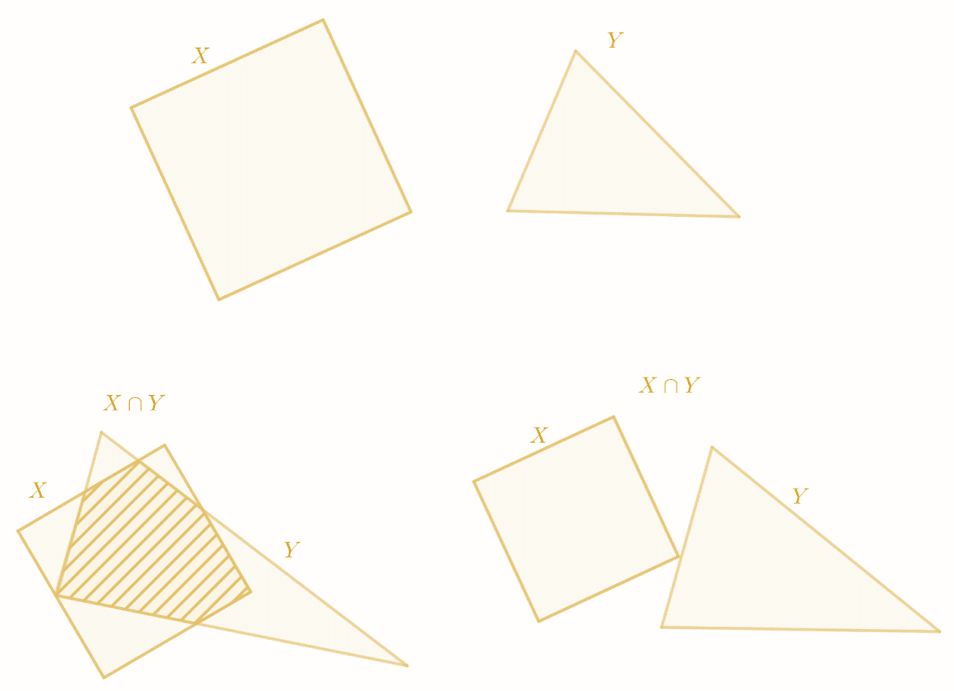
En dibujo, a la derecha se muestra la intersección de conjs (disjuntos) que no tiene elementos en común, y a la izquierda conjs (que se intersecan) que sí tienen elementos en común. El elemento z se encuentra en el área remarcada.

Por ejemplo:

si \(X = \){\(1, 7\)} y \(Y = \){\(2, 7\)}

Aquí el elemento que se repite es el número 7. Ya que aparece en ambos conjs.

\(X ∩ Y = \){\(1, 7\)}\(∩\){\(2, 7\)} \(= \){\(7\)}

Diferencia o resta

\(X ∖ Y = \){\((z ∊ X) ∧ (z ∉ Y)\)}

En español esto quiere decir: \(z\) es un elemento que está en el conj \(X\) y \(z\) no es un elemento del conj \(Y\).

-Otra forma de decirlo, la resta es quitar a un conj los elementos de otro conj.-

El orden en que se hace la diferencia o resta es muy importante. No es lo mismo hacer \(X ∖ Y\) que hacer \(Y ∖ X\).

Por ejemplo:

\(Si X = \){\(1, 3, 5, 7\)} y \(Y = \){\(1, 2, 3, 4, 5, 6, 7, 8, 9\)}

Entonces:

X ∖ Y = {1, 3, 5, 7} \ {1, 2, 3, 4, 5, 6, 7, 8, 9} = ∅

En este caso TODOS los elementos de X también son elementos de Y. Es decir, X ⊂ Y. Entonces al terminar de hacer la operación y quitar los elementos que están en ambos conjs el conjunto al que debemos de revisar se quedó sin nada. Por lo que el resultado es el vacío.

Y ∖ X = {1, 2, 3, 4, 5, 6, 7, 8, 9} \ {1,3,5,7} = {2, 4, 6, 8, 9}

Caso contrario ocurre aquí. Quitamos todos los elementos que hay en común entre X y Y, los elementos en comunes entre estos dos conjs son {1, 3, 5, 7}.

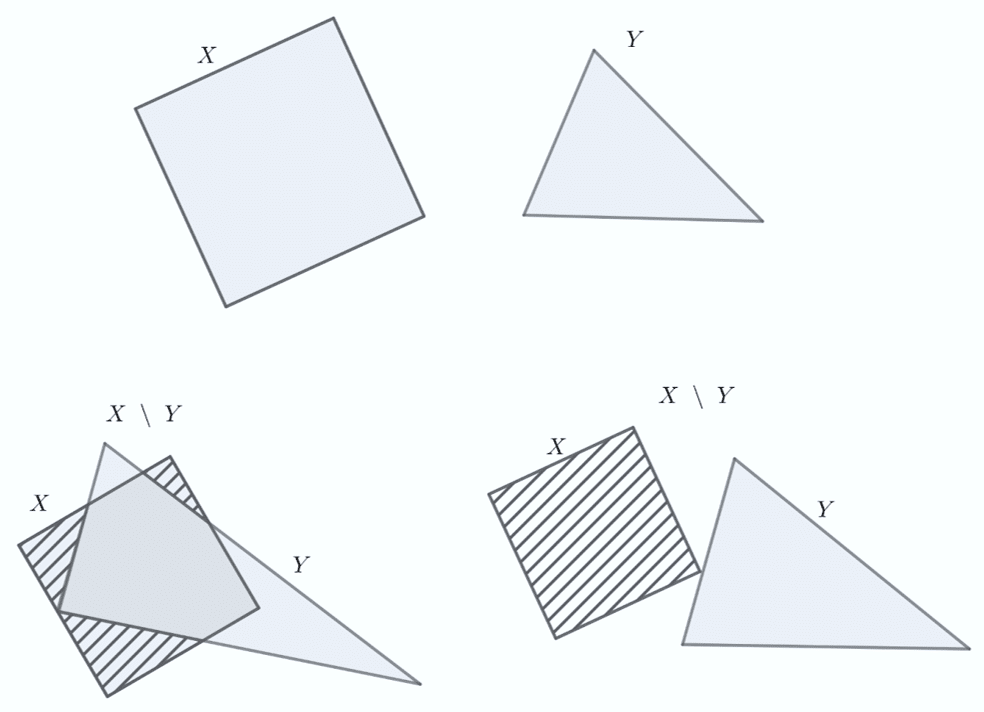
En dibujo, a la derecha se muestra la diferencia o resta de conjs (disjuntos) que no tiene elementos en común, y a la izquierda conjs (que se intersecan) que sí tienen elementos en común. El elemento z se encuentra en el área remarcada.

Diferencia simétrica

• X ∆ Y = z ∊{(X ∪ Y) ∖ (X ∩ Y)} = z ∊{(X ∖ Y) ∪ (Y ∖ X)}

En español esto quiere decir: z es un elemento que está en el conjunto X o z es un elemento del conjunto Y, pero no es un elemento de X y Y a la vez.

-Esta operación nos dirá los elementos que están en la unión de X y Y, pero no son elementos de la intersección de X y Y.-

La diferencia simétrica es una combinación de la unión y la resta de conjs, o también puede serlo de la unión, intersección y la resta de conjs. 

Como ejemplo:

-Si X = {1, 3, 5, 7} y Y = {1, 2, 3, 4, 5, 6, 7, 8, 9}, entonces la diferencia simétrica X ∆ Y se puede hacer en los siguientes pasos:

Escogemos una de las dos formas:

X ∆ Y = {(X ∖ Y) ∪ (Y ∖ X)}

Hacemos las operaciones que están entre los paréntesis:

X ∖ Y = {1, 3, 5, 7} \ {1, 2, 3, 4, 5, 6, 7, 8, 9} = ∅

Y ∖ X = 1, 2, 3, 4, 5, 6, 7, 8, 9} \ {1, 3, 5, 7}={2, 4, 6, 8, 9}

Por último sustituimos:
X ∆ Y = {(X ∖ Y) ∪ (Y ∖ X)} = {({1, 3, 5, 7} \ {1, 2, 3, 4, 5, 6, 7, 8, 9}) ∪ ({1, 2, 3, 4, 5, 6, 7, 8, 9} \{1, 3, 5, 7})} = ∅ ∪ {2, 4, 6, 8, 9} = {2, 4, 6, 8, 9}

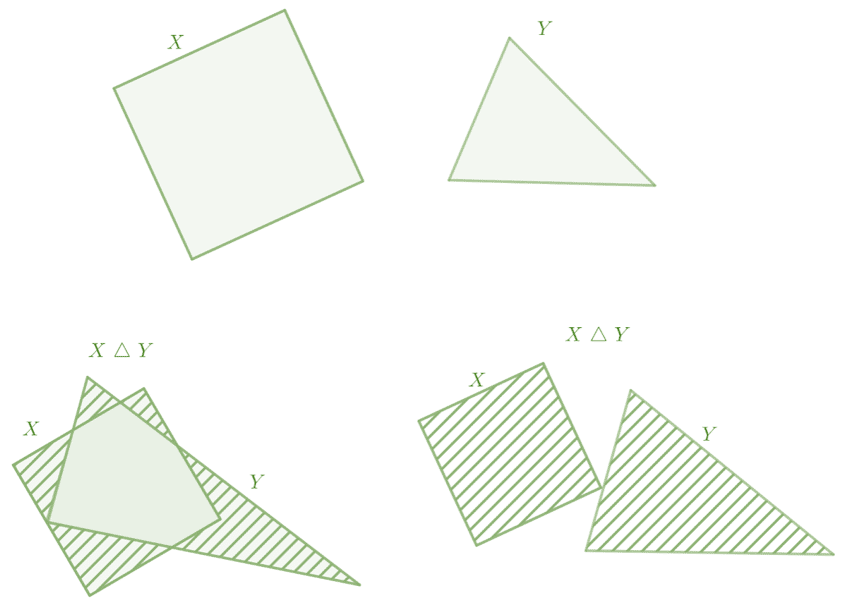
En el dibujo, a la derecha se muestra la diferencia simétrica de conjuntos (disjuntos) que no tiene elementos en común, y a la izquierda conjuntos (que se intersecan) que sí tienen elementos en común. El elemento z se encuentra en el área remarcada.

-¿Quedará el mismo resultado si usamos la otra definición?-

Y eso es todo lo esencial para poder trabajar con los conjuntos de una manera sencilla e introductoria. Espero que estas entradas les hayan sido de ayuda y también que puedan acompañarnos cuando abordemos los siguientes temas.

Aceptamos comentarios, quejas y sugerencias sobre los temas, ya sea en mi correo personal (al final del blog) o en la caja de comentarios. ¡Gracias por llegar hasta el final!

-Como regalo y ejercicio de despedida.-

De la siguiente imagen, nombre a los conjs (como tú quieras) y dibuja la diferencia simétrica eligiendo 2 o más conjs.

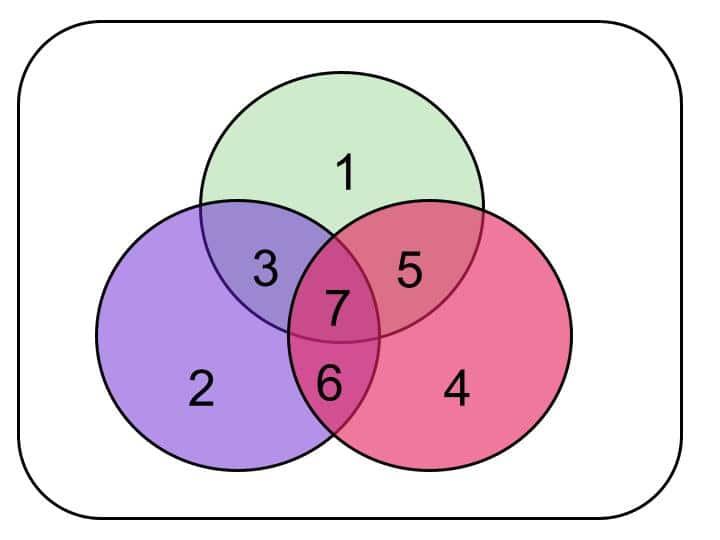
Un saludo a todos.

¿Quieres saber más?

Hernández, F. (2019), “Teoría de conjuntos Una introducción”, Instituto de Matemáticas, 2ª ed., pp. 5–21.

UNAM. Lipschutz, S. (1970), “Teoría de conjuntos y temas afines”, McGRAW-HILL, 1ª ed., pp. 1–17.