Como buen mexicano que soy, vengo a enseñarte palabrotas en este idioma llamado matemáticas.
Seguramente en algún momento de nuestra educación básica, especialmente en secundaria o preparatoria, nuestros maestros nos empezaron a decir groserías o palabras rimbombantes en clase de matemáticas. Algunos ejemplos que quizá recuerdes sean: conjunto, relación, factorización, funciones, cateto, permutación, hipotenusa, integral, etc.
Esto se debe a un hecho al que rara vez se le dedica tiempo en el aula y es el papel de las definiciones en matemáticas.
Parafraseando a John B. Fraleigh:
“Esta importancia surge, en gran parte, por la necesidad de los matemáticos de comunicarse de manera eficiente. Si dos o más personas tratan de intercambiar opiniones sobre un tema y tienen distintas ideas acerca del significado de términos técnicos o de uso cotidiano en su trabajo podrían surgir malos entendidos, fricciones y quizás podría correr sangre. Por lo que en matemáticas debemos evitar las ambigüedades.”
De esto tratarán futuras entradas: dando las definiciones, iremos explicando y desglosando de la manera más natural, simple e intuitiva posible sin perder mucho la formalidad que exigen algunas de las groserías más comunes que se encuentran en matemáticas.
Los números
Una de las primeras y más importantes preguntas que nos podemos hacer desde muy temprana edad es: ¿Qué son los números?, la cual no es una pregunta sencilla ya que existen muchas cosas a las que podemos llamarle números.
La noción más básica de lo que es un número la encontramos en listar o enumerar cosas.
La idea es bastante primitiva, tanto como los primeros grupos de humanos que se vieron en la necesidad de juntar objetos que tuvieran cosas en común y que se podían distinguir unos de otros. Es decir, describir cantidades, por ejemplo: CERO caballos, UNA persona, DOS días, CINCO abejas, QUINCE años, etc…
A este tipo de números los llamamos números naturales y al conjunto de estos números lo escribimos con está letra ℕ.
Existen varias maneras describir/definir a los ℕ en notación matemática:
ℕ≔{𝑥 ∈ ℝ | 𝑥 es elemento de un conjunto inductivo.}
ℕ≔{n : n es natural.}
ℕ≔{0, 1, 2, 3, 4, 5, …}
Este símbolo (∈) se llama épsilon, una letra griega que en algún momento de la historia de las matemáticas se comenzó a utilizar con el significado de *PERTENECE A*. Tanto los dos puntos (:), y las barra (|) se leen o entienden con la frase *TALES QUE* cumplen la regla o propiedad que se menciona después de ellas.
Las tres definiciones anteriores son válidas, pero para evitar confusiones por el momento nos quedaremos con la definición más terrenal: la última.
Los ℕ tienen muchas propiedades importantes como es el empezar con el elemento cero “0”, el cual representa la ausencia o no existencia de algo [algunos matemáticos no están de acuerdo con esto, pero es una tema que se explicará en futuras entradas]. Asimismo, con ellos podemos realizar las operaciones de suma o adición (+) y la multiplicación o producto, que puede bien escribirse con una (×) , un (∗), o incluso un (•).
Estrictamente hablando no podemos hacer las operaciones de resta (-), ni división (/), o (÷) porque la gran mayoría de sus resultados no son números que estén dentro de la cajita de los números ℕ.
Otra pregunta natural después de leer el párrafo anterior es: ¿Qué son las operaciones?, ¿Qué es la suma?, ¿Qué es la multiplicación?
Formalmente hablando las operaciones son relaciones que eligen dos o más elementos de un conjunto, en este caso de ℕ, y el resultado es otro elemento de ℕ.
Con esta idea en mente ahora nos preguntamos de manera particular:
¿Qué es la suma?
En notación matemática:
+ ∶ ℕ×ℕ → ℕ
(a, b) → a + b
En español, lo anterior se interpreta como:
Digamos que a=3 y le damos el color rojo, mientras que b=4 y le pintamos de azul. La suma se podría ver de la siguiente manera.
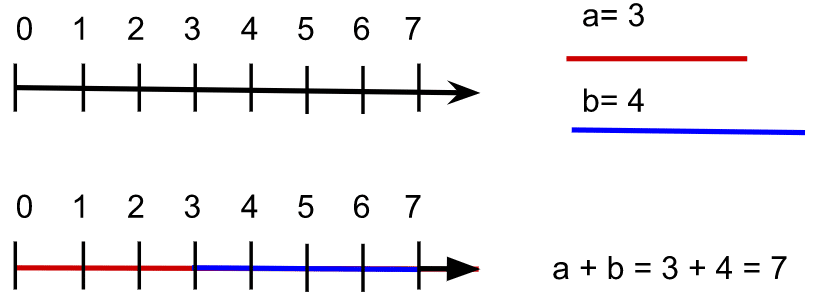
Esto simplemente significa que le digamos a las letras a y b que elijan un número de los que están la bolsita de los ℕ y un color para poder distinguirlas, luego pedimos a la a que se acomode al inicio de la recta, es decir, en el cero, y avance hasta el número que escogió.
Después b hace lo mismo, pero debe empezar en donde terminó a. De esta forma, la suma es el número al que se llega si caminamos por las zonas que tengan los colores rojo y azul.
Siguiendo la misma línea de pensamiento, nos podemos preguntar:
¿Qué es la multiplicación?
En notación matemática:
•∶ ℕ×ℕ → ℕ
(a,b) → a•b
La expresión anterior se interpreta, en español, como:
Digamos que a=3 y le damos el color rojo mientras que b=2 y le pintamos de azul. La multiplicación se podría ver de la siguiente manera.
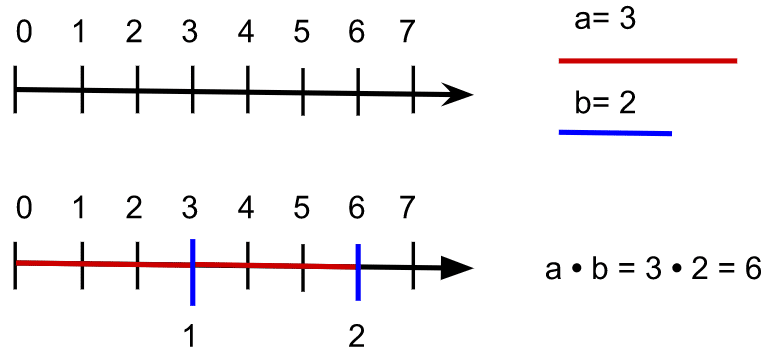
Una forma de entender la multiplicación es como una suma rápida, es decir:
Le decimos a las letras a y b que elijan un número de los que están la bolsita de los ℕ y un color para poder distinguirlas, luego pedimos a la a que se acomode al inicio de la recta, en el cero, y avance hasta el número que escogió. Después le pedimos a esa misma a que se sume a sí misma b-veces (el número que eligió b). Cada vez que terminamos de sumar una a dibujamos una marca del color de b al resultado de esa suma. La multiplicación es el número al que se llega si caminamos por las zonas que tengan colores al terminar todas las sumas pequeñas.
Y ¡VOILÀ!, hemos logrado representar a los números más antiguos que se conocen, aquellos que nacieron de las necesidades más básicas de las antiguas civilizaciones. Este es el primero de muchos pasos para poder entender las bellas ideas que se esconden detrás de las groserías que rara vez nos detenemos a explicar.
No os espantéis al ver esto. Las ideas se volverán más claras conforme las entradas del blog avancen y expliquemos detalladamente otras palabrotas como: conjunto, relaciones, funciones, etc. Las cuales son las bases para construir casi la totalidad de las ideas que sostienen el lenguaje y la lógica de las matemáticas actuales.
¿Quieres saber más?
Aguilar Márquez, A., et al. (2008), “Matemáticas simplificadas”, Pearson Prentice-hall, CONAMAT.
Linares García, R. et al., (2015), “Matemáticas elementales”, Textos Científicos, BUAP, vol. 1: 133-135.
Fraleigh, J. B. & Katz, V. J. (2003). “A First Course in Abstract Algebra“. Addison-Wesley.