Teniendo ya una idea de lo que es un axioma y un conjunto (si no has leído la primera parte de la entrada, te invito a revisar ¿De qué están hechas las matemáticas?), ahora podemos enunciar los primeros axiomas. También haremos una distinción entre dos formas en las que se pueden enunciar.
En algunos casos marcaremos un axioma con la palabra débil o simple. Con esto queremos decir que la forma en la que se escribió no es muy formal, pero en esencia (que es lo importante) dice exactamente lo mismo que el axioma «fuerte» o «completo«.
Dato cultural: Por lo general los matemátic@s somos personas flojas, y se nota mucho al momento de escribir. Eso no significa que no hagamos bien las cosas; sino que nos gusta ahorrar palabras usando símbolos o abreviaturas. Por lo que, de ahora en adelante abreviamos a los Axiomas cómo: Ax en singular o Ax’s en plural. Lo mismo haremos con los conjuntos como: conj en singular y conjs para el plural.
1) Ax. «débil» de Existencia.
Existe al menos un conjunto.
Para poder hablar y trabajar con los conjuntos debemos SUPONER / ESTABLECER que existen.
La línea de pensamiento que podemos seguir para entender este Ax sería:
-Si existe al menos un conjunto. Este puede ser como yo me lo quiera imaginar.–
-¿Cuál es el conjunto más sencillo que podría existir?-
Después de meditarlo un rato podríamos llegar a la idea de que el conj más simple es el que no tiene nada.
1.1) Ax. de Existencia.
Hay un conjunto que no tiene elementos.
El único conjunto que no tiene elementos es llamado el “conjunto vacío”, “el vacío” o simplemente “vacío” y lo denotamos por ∅.
Si nos imaginamos al vacío como alguna de estas cosas, al final de pensarlo un rato no tendrías nada. Porque eso es precisamente lo que representa el vacío.
-Y si, por el contrario al vacío, ¿qué puedo hacer si tengo muchos conjuntos y no quiero dibujar muchas mochilas, bolsas o contenedores?-
-Buena pregunta.-
Otro modo de hacerlo es dibujar a los conjuntos como figuras planas, que podemos etiquetar con su nombre para distinguirlos mejor. Por lo general se usan solo círculos y óvalos por simplicidad. Pero nada estricto ni necesario.
2) Ax. de Extensión.
Si todo elemento de X es elemento de Y, y todo elemento de Y es elemento de X entonces X=Y.
-¿Pero qué significa el revoltijo de arriba?-
En palabras normales: Dos conjuntos que tienen exactamente los mismos elementos son iguales (idénticos).
Ejemplo de la notación:
X=Y sii (∀ x : x ∈ X ⇒ x ∈Y) ∧ (∀ x : x ∈ Y ⇒ x ∈ X)
El sii es un operador lógico y se lee como «sí y solo sí», también se puede escribir con el símbolo «⇔» y nos sirve para indicar que la afirmación X=Y que está a la izquierda solo puede ser cierta cuando se cumple la notación de la derecha: (∀ x : x X ⇒ x ∈ Y) ∧ (∀ x : x ∈ Y ⇒ x ∈ X).
Y lo mismo al revés, si ocurre (∀ x : x ∈ X ⇒ x ∈ Y) ∧ (∀ x : x ∈ Y ⇒ x ∈ X) entonces debe ocurrir que X=Y
Una forma de verlo con dibujo podría ser la siguiente:
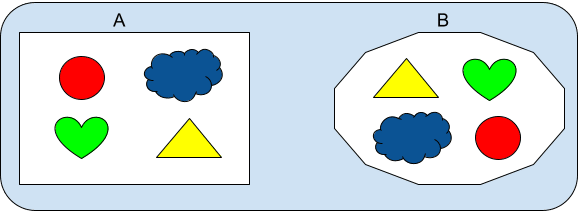
En este ejemplo A = {❤,○, ☁, △} y B = {☁, △, ❤,○}
Tanto A como B tienen las mismas figuras, los mismos colores, y las mismas figuras con los mismos colores. Aquí NO importa el orden en el que se escriben a los objetos (elementos), lo que importa es cuántos de esos elementos son diferentes.
Por hoy terminamos con los dos axiomas, así que cerremos el tema aquí para que vayas por un café, pero esto aún no ha acabado…
¿Quieres saber más?
Hernández, F. (2019), “Teoría de conjuntos Una introducción”, Instituto de Matemáticas, 2ª ed., pp. 5–21.
UNAM. Lipschutz, S. (1970), “Teoría de conjuntos y temas afines”, McGRAW-HILL, 1ª ed., pp. 1–17).



