¿De qué están hechas las matemáticas?

-Primero que nada, ¿Qué es un axioma?-

-¿Un qué…?-  

– Un axioma. –

Según la RAE: Es una proposición tan clara y evidente que se admite (acepta) sin demostración (pruebas).

Dicho de otro modo: Son afirmaciones que se dan por hecho.

Y en matemáticas este tipo de proposiciones o enunciados son muy, muy importantes, con ellos se construyen los cimientos lógicos en los que se sostienen las teorías matemáticas. Es decir, los axiomas son los responsables de darle forma y fuerza a las matemáticas.

Seguramente ya te has topado con este tipo de enunciados durante la secundaria o bachillerato, pero con otros nombres. Uno de los ejemplos más conocidos son “Los postulados de Euclides” en geometría.

Para Euclides existen “cosas” que simplemente son, “cosas” que no podemos describir de maneras más simples. Entre esas “cosas” están los conceptos de punto, línea y plano.

-Pero… ¿Qué es un punto?, ¿Qué es una línea?, ¿Qué es un plano?-

• El punto es lo más simple o pequeño que existe en La Geometría. no se puede deshacer al punto en cosas más pequeñas o sencillas.

• La línea es una “fila” que se arma poniendo puntos uno junto a otro tan pegados de modo que no hay espacio para poner otro punto entre ellos.

• El plano es un montón de líneas “pegadas” una al lado de otra de forma que no quepa un punto entre línea y línea. Si cabe un punto podemos pegar más puntos hasta formar otra línea y llenar ese hueco.

Como ejemplo, dos de Los Postulados de Euclides:

1. Dos puntos distintos cualesquiera determinan un segmento de recta.

(Si dibujas dos puntos puedes dibujar una línea recta infinita que los une).

Esta es una afirmación o proposición que se puede mostrar haciendo dibujos. 

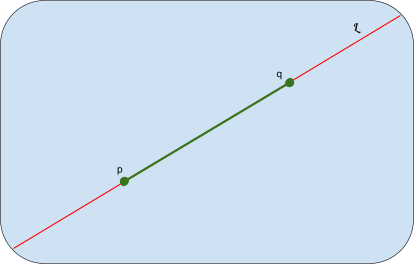
ւ es la línea recta infinita que pasa por los puntos p y q.

2. Todos los ángulos rectos son iguales entre sí.

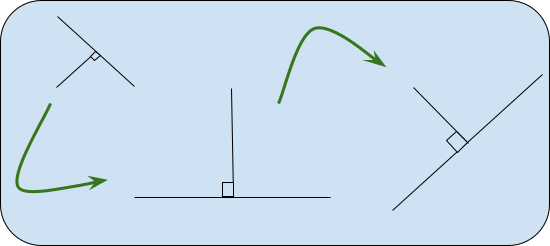
Podríamos recortar está afirmación a : “Todos los ángulos rectos son iguales”. No importa el tamaño o las posiciones de las líneas que forman el ángulo recto.

Lo que haremos será desarrollar (en está y siguientes entradas del blog) ideas muy similares a las de Euclides, pero usando a los conjuntos.

-Hablando de… ¿Qué ^€®£∆ es un conjunto?-

Lo que la gente normal entendemos de lo que es un conjunto es una idea similar a la de lo que entendemos que es un punto, una línea o un plano. Es de esas ideas que es más fácil mostrar lo que son que explicarlas.

Al hablar o al usar a los conjuntos tendremos 3 puntos/convenciones a considerar.

• Por un conjunto entenderemos una colección de objetos o cosas bien definidas (de forma que no pueda ocurrir que un objeto o cosa en particular pertenezca y no pertenezca a ella a la vez).

• Se escribe a los conjuntos con letras mayúsculas (A, B, C, … X, Y, Z) y a los elementos de estos conjuntos con minúsculas (a, b, c, … , x, y, z) (esto no es estricto ni necesario pero es muy útil para hacer una distinción al momento de escribir).

• Es normal pensar en un conjunto que tiene a la mayoría de los objetos con los que queremos trabajar. Generalmente se le suele denominar como conjunto Universo y es común escribirlo con una 𝒰, pero puede variar dependiendo del área en que se esté trabajando.

Por ejemplo: 𝒰 sería el conjunto de las figuras geométricas si hablamos de los triángulos, cuadrados, pentágonos o polígonos en general. Por otro lado, si nos interesa contar, nuestra 𝒰 sería el conjunto de los números naturales ℕ, etc. 

Una forma de visualizar a los conjuntos como algo tangible, es poder imaginarlos como bolsas, cajas, cubetas, mochilas o algún otro tipo de contenedor en los que podemos poner sus elementos.

-Espera, espera, ¿Y la imaginación?-

-Ah cierto. La imaginación.-

Sí, aunque sea difícil de creer, las matemáticas empiezan desde la imaginación. Como lo hemos mencionado en el párrafo anterior. Si no podemos crear una imagen de una idea o cosa en nuestras mentes, será más complicado hacer algo con esas ideas.

¡Y LISTO!, estas son las piezas con las que armamos las ideas en matemáticas. De aquí en adelante los conjuntos nos dirán los ingredientes con los que podemos trabajar y los axiomas nos dirán “el cómo” es que podemos usarlos. Lo demás es paciencia e imaginación.

¿Quieres saber más?

Hernández, F. (2019), “Teoría de conjuntos Una introducción”, Instituto de Matemáticas, 2ª ed., pp. 5–21.

UNAM. Lipschutz, S. (1970), “Teoría de conjuntos y temas afines”, McGRAW-HILL, 1ª ed., pp. 1–17).