Mi cumpleaños es el 29 de septiembre. ¿Y el tuyo cuándo? Tal vez te suene raro, pero es imposible (al menos desde el mundo de los números) que falte exactamente un año para tu cumpleaños. A continuación vamos a demostrarlo con estos tres sencillos pasos:
| Pasos | Ejemplo |
|---|---|
| 1. Piensa la fecha de tu cumpleaños. | En mi caso, el 29 de septiembre. |
| 2. Ahora imagina el día siguiente de tu cumpleaños, faltan exactamente 364 días para tu siguiente cumpleaños. | El día siguiente es el 30 de septiembre y faltan exactamente 364 días para el siguiente 29 de septiembre. |
| 3. Pero el día anterior a tu cumpleaños falta solamente 1 día. | El día anterior es el 28 de septiembre y falta 1 día para el 29 de septiembre. |
Pero lee con cuidado, porque lo que nos está diciendo esta tabla es que el único día que puede faltar precisamente 1 año para tu cumpleaños es el mero día de tu cumpleaños, pero eso es imposible.
¡¡¡No puede faltar 1 año para un día que ya estás viviendo!!!
Mágicamente (aparentemente) hay un salto del día 1 al día 364, pero ¿por qué sucede esto? La respuesta requiere de nociones de Álgebra Abstracta, pero intentaré dar un efectivo resumen.
Primero, te presento a los grupos cíclicos finitos (no te espantes con los símbolos, céntrate en los figurines):
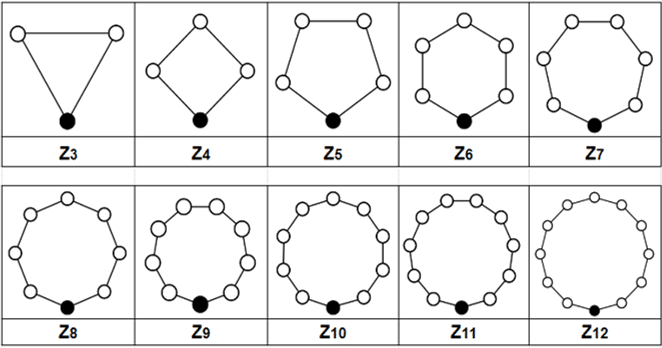
Figura 1. Ejemplos de grupos cíclicos finitos.
Pon la punta de tu dedo en el círculo negro de alguna de las imágenes de arriba; después, avanza en la misma dirección las veces que el numerito del subíndice de la Z te dice. Por ejemplo, yo elegiré Z10.
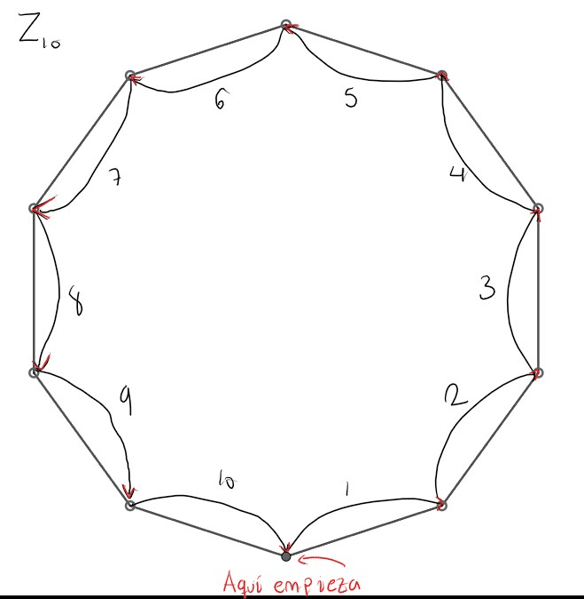
Figura 2. Ejemplo particular con Z10.
En teoría, sin importar cual imagen elegiste, debiste llegar de nuevo al círculo negro (si esto no pasó, sigue el ejemplo de arriba). El punto negro se puede interpretar como el número cero y avanzar en el mismo sentido es como sumar un 1 (por consiguiente, retroceder es como restar 1). Observa que en Z10: 1+1+1+1+1+1+1+1+1+1 = 0 (círculo negro).
En pocas palabras, un grupo es un conjunto (en este caso de puntos, el círculo negro y los círculos blancos) tal que tiene tres propiedades:
- Una operación (“avanzar” o “retroceder” en este ejemplo).
- Un elemento neutro (el punto negro).
- Y que desde todo punto puedes avanzar o retroceder lo suficiente para llegar al punto negro (Nota: si estás en el punto negro avanzas o retrocedes cero movimientos para llegar al mismo).
Ahora, se dice que un grupo es cíclico cuando se pueden recorrer todos sus puntos con el dedo sin despegarlo de la figura (lo que matemáticamente sería sumar números 1). ¿Cuál es el grupo cíclico en la Figura 3?
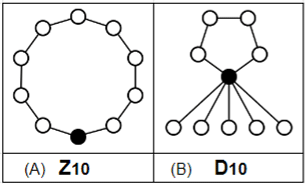
Figura 3. (A) Grupo cíclico y (B) grupo no cíclico.
Si es que no te he aburrido con mis números y puntos, te pido por favor que imagines el día de tu cumpleaños como el punto negro y que la propiedad de avanzar sea el pasar de los días (tristemente en este caso no podemos retroceder el calendario, ya que hasta ahora no hay viajes en el tiempo 🙁 ), por lo que al año le corresponde el grupo Z365. Y sí, el sumar 1 consigo mismo 365 veces es igual a cero, porque el año es un grupo cíclico. Este es el motivo analítico (una forma demasiado elegante de decir que el método lleva muchas cuentas) por el cual no puede faltar un año para tu cumpleaños.
Pero los grupos cíclicos no son una curiosidad matemática, son algo que se usa tanto en la teoría matemática (aparecen en todos lados, desde la topología hasta en teoría de números) como en el día a día. Por ejemplo: en el reloj de 12 horas, en la criptografía o en la famosa frase “nos vemos de hoy en ocho”.
Las matemáticas no son algo ajeno a nosotros, sino que están conectadas con nuestro día a día, desde cosas muy complejas hasta tu feliz cumpleaños. Σ
Agradecimientos
Agradezco a Aslhy Pastor, Francisco López y a Sujeto (alias conejito Pepito) por sus comentarios y correcciones al borrador de esta entrada, y a mi madre por ser un gran apoyo para mí.
¿Quieres saber más?
Rotman J. (1984), «An Introduction to the Theory of Groups«, Springer New York, NY.
Lidl R., Pilz G. (1998), «Applied Abstract Algebra«, Springer New York, NY.



