Listo, regresamos de un breve descanso para seguir hablando de axiomas y conjuntos… Aquí vamos con un nuevo axioma…
6) Ax. “débil” del conjunto Potencia.
Para cualquier conj T existe un conjunto P tal que X ⊆ T implica X ∈ P.
Llamamos a T el conjunto de TODOS los subconjuntos de X y es denotado por 𝓟 (X).
-¿Subconjunto?, ¿Qué es eso?-
-Muy fácil, un subconjunto es un conj que está contenido en otro conj.-
De hecho ya vimos ejemplos de subconjuntos en la anterior entrada. Si aún no la has leído, te invito a revisarla en Armando conjuntos.
Ahora, veamos un ejemplo de esto con gatitos:
Digamos que T={ {😸}, { {😸} } }. El conjunto de los gatitos que están dentro de una casa. T es un conj que solo tiene dos elementos; {😸} y { {😸} }, ahora debemos nombrar a estos dos conjuntos.
t1= {{😸}} es el conjunto del gatito dentro de una caja y t2= { {{😸}} } es el conj del gatito que está dentro de dos cajas, t1 y t2 son elementos de T, pero también son conjs por sí mismos.
t1 ⊂ T y t2 ⊂ T.
El símbolo “⊆” o “⊂” significa “subconjunto de”, y juega un papel muy similar al de “𝜖” porque nos dice que ese elemento (que también es un conj) está contenido en el conj más ”grande”.
Estos no son todos los Subconjs de T.
Por definición el ∅ y el “total” (en este caso el conj T) son subconjs de todo conj.
Si en el párrafo anterior cambiamos a las letras por el contenido de los conjuntos y agregamos al vacío y al total quedarían como en la siguiente tabla:
| t1 ⊂ T | y | t2 ⊂ T |
|---|---|---|
| {{😸}} ⊂ { {😸}, { {😸 } } } | y | { {{😸 }} } ⊂ { {😸}, { {😸 } } } |
| {{😸}} ⊂ { {😸}, { {😸 } } } | y | { {{😸 }} } ⊂ { {😸}, { {😸 } } } |
| ∅ ⊂ { {😸}, { {😸 } } } | Por la definición | |
| { {😸}, { {😸 } } } ⊂ { {😸}, { {😸 } }} | Por la definición |
-Listo, esos son los subconjuntos de un conjunto de 2 elementos.-
-¿En dónde nos habíamos quedado? Ah, sí, LA POTENCIA.-
Lo interesante o curioso de la potencia de un conj es que juega a mezclar a sus elementos.
-¿Cómo que juega con sus elementos?-
-Aunque suene raro, lo hace copiando, cortando y pegando.-
La potencia toma al conj, observa todos sus elementos, los parte y los va copiando y pegando en subconjuntos. El orden en el que lo hace es lo bonito.
Imaginemos al Conj A = {♠, ♦, ♣}.
Para este caso en particular (3 elementos) nos conviene ver al conj potencia como un cajón largo con divisiones.
El orden en que se harán estas operaciones no es necesario; al conjunto no le importa el orden en que se escriban sus elementos. Pero es bueno hacerlo de este modo para no confundirse.
En el primer espacio ponemos al ∅ y en el último al conj original o total {♠, ♦, ♣} quedando algo así:
| ∅ | {♠, ♦, ♣} |
Para encontrar a los elementos que van en medio tenemos que volver a copiar al conjunto original y partirlo en todos sus elementos individuales:
{♠, ♦, ♣} → {♠}, {♦}, {♣}.
Después estos se colocan en las casillas inmediatas al ∅, quedando de la siguiente manera:
| ∅ | {♠} | {♦} | {♣} | {♠, ♦, ♣} |
Ahora hacemos una copia de los elementos individuales y usando el Ax. de la unión los juntamos todos contra todos en pares.
{♠} ∪ {♦} = {♠, ♦} = {♦} ∪ {♠}.
{♠} ∪ {♣} = {♠, ♣} = {♣} ∪ {♠}.
{♦} ∪ {♣} = {♦, ♣} = {♣} ∪ {♦}.
| ∅ | {♠} | {♦} | {♣} | {♠, ♦} | {♠, ♣} | {♦, ♣} | {♠, ♦, ♣} |
El resultado (en este caso particular) después de hacer todas las uniones y agregarlas a los espacios faltantes del cajón es el conjunto Potencia de A:
𝓟 (A) = 𝓟 ({♠, ♦, ♣}) = {∅, {♠}, {♦}, {♣}, {♠, ♦}, {♠, ♣}, {♦, ♣}, {♠, ♦, ♣}}.
Repasemos algunos ejemplos de la Potencia usando figuras:
| 𝓟 (∅) = ∅. La potencia del vacío sigue siendo el vacío porque no tenemos elementos que podamos juntar entre ellos. |  |
| 𝓟 ({a})= {{a}, ∅}. La potencia de un conjunto que solo tiene un único elemento es el conjunto que tiene al vacío y el que tiene a ese otro elemento. |  |
| 𝓟 ({a,b})= {{a,b},{a},{b},∅}. La potencia de un conjunto con dos elementos es el conjunto que contiene al vacío, a esos dos elementos por separado y a los dos elementos juntos (Aquí estaría el ejemplo de los gatitos de arriba). | 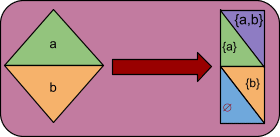 |
–¿Pueden dibujar el ejemplo de A = {♠, ♦, ♣} con figuras y colores?–
Cerremos el cuaderno por hoy, pero te esperamos la siguiente semana para concluir con el tema…
¿Quieres saber más?
Hernández, F. (2019), “Teoría de conjuntos Una introducción”, Instituto de Matemáticas, 2ª ed., pp. 5–21.
UNAM. Lipschutz, S. (1970), “Teoría de conjuntos y temas afines”, McGRAW-HILL, 1ª ed., pp. 1–17).



